Üslü sayılarda toplama nasıl yapılır? Üslü ifadelerde toplama-çıkarma işleminin kuralı nedir? Formülü var mıdır? Burada tüm bu soruların yanıtını bulacaksınız.
Sevgili gençler, üslü sayılarda toplama işlemini (ya da çıkarma işlemi) tıpkı diğer konularda olduğu gibi basit bir yöntemle artık çok kolay yapabileceksiniz. Bu yöntem hepimizin çok yakından bildiği ve çarpanlara ayırma konusundan tanıdığı “ortak paranteze alma” işlemidir.
Üslü sayılarda toplama nasıl yapılır?
Üslü sayılarda toplama yapmak için aşağıdaki maddeleri uygulamanız yeterli olacaktır. Doğru sanılan ama kesinlikle çok sakıncalı olan ilk iki maddeye özellikle çok dikkat edin. Üslü sayılarda toplama (ya da çıkarma) işleminde
- tabanlar aynıysa “üsler toplanır” diye bir durum yoktur, yanlıştır.
- üsler aynıysa “tabanlar toplanır” diye bir durum da yoktur, yanlıştır.
- üslü ifadeleri hesaplamak kolaysa her birinin değeri bulunup toplama-çıkarma işlemi yapılabilir.
- üslü ifadeler hesaplanamayacak kadar büyükse ya da zaman alacak türden ise, tabanların ortak çarpanı olup olmadığı kontrol edilir.
- tabanların ortak çarpanı yoksa çözümü için üslü sayılardan başka yollar düşünmelisiniz.
- tabanların ortak çarpanı varsa, ortak paranteze alma işlemini kullanabilirsiniz.
- tabanlar aynı üsler farklıysa ortak paranteze alma işlemi düşünülebilir.
- taban ve üs aynıysa üslü ifadelerin önündeki katsayıların toplama/çıkarma işlemiyle sonuca gidilebilir.
Bunu görmelisin
Üslü sayılarda ortak paranteze alma
Ortak paranteze alma işlemini bilmeden üslü ifadelerde toplama / çıkarma işlemlerini yapmanız bazı sorularda saatlerinizi alabilir. İşlemi kolay olan sorularda örneğin,
23 + 34 – 82 = ?
gibi sorularda, üslü ifadelerin değeri hesaplanabilecek kadar küçük olduğu için ortak paranteze ihtiyaç duymayız.
Fakat örneğin
96 + 95 işleminin %10’u kaçtır?
gibi hesaplaması oldukça zaman alıcı olan üslü sayılarda toplama işlemini ortak paranteze alarak çok kısa sürede çözebilirsiniz.
Üslü sayılarda ortak paranteze alarak çözülen ifadeler
Üslü sayılarda ortak paranteze alma yapabilmenin tek şartı toplama/çıkarma işlemi ile tabanlarda ortak çarpan olmasıdır.
Örneğin aşağıdaki üslü ifadelerde yer alan toplama ve çıkarma soruları ortak paranteze almaya uygundur.
- 58 – 57 + 56 – 55
- 109 – 108 + 107
- 95 – 65
- 6n + 3n
- 10n+1 – 10n + 10n-1
- x2n – xn+1
Oysa ki aşağıdaki örneklerde yer alan üslü ifadelerde tabanların ortak çarpanı olmadığı için toplama ya da çıkarma işlemini yapabilmek için ortak paranteze alma işleminden yaralanamayız.
- 310 – 210
- 310 – 210
- a4 + b4
- 10n – 9n
- xy + yx
- 78 + 87
Yukarıdaki üslü ifadelerin hiç birinde ortak çarpan bulunmadığı için ortak paranteze alma işlemi uygulayamayız. Evet toplama ve çıkarma işlemleri var ama bu, ortak paranteze alabilmek için tek başına ne yazık ki yetmiyor.
Bunu görmelisin
Üslü sayılarda toplama işlemi
Üslü sayılarda toplama işlemini ortak paranteze alarak nasıl yapacağımızı bir kaç örnekle gösterelim.
ÖRNEK 1:
(1011 – 1010)/9
işleminin sonucu kaçtır?
ÇÖZÜM :
Çıkarma işleminin olduğu üslü sayıların en büyük ortak çarpanı 1010 dur. Parantez içindeki ifadeyi 1010 parantezine alalım.
1010 . (10 – 1)/9
( 1010 . 9) / 9
Yukarıdaki 9’lar sadeleşir ve sonuç
1010 olur .
ÖRNEK 2:
(67 + 37)/129
işleminin sonucu kaçtır?
ÇÖZÜM :
Bu soruda üslü sayılarda toplama işlemi göze çarpıyor. Bu toplama işlemini uzun yoldan yani sayıları tek tek bulmaya çalışarak çözersek inanın çok vaktinizi alır. Üstelik işlem hatası yapıp boşa zaman harama riski de var.
Madem tabanlardaki sayıların ortak böleni (çarpanı) var o halde ortak paranteze alma ile sonuca gidebiliriz. En büyük ortak bölen 37 sayısının parantezine alalım.
37 . ( 27 + 1) / 129
37 . 129 / 129
129’lar sadeleşirse sonuç 37 olur.
Bunu görmelisin
Üslü sayılarda toplama işleminde harf olursa ne yapmalıyız?
Üslü sayılarda harf olup olmaması önemli değil, yeter ki tabanlardaki sayıların ortak böleni olsun. Örneğin aşağıdaki tüm ifadelerde ortak çarpan içerenlerin ortak paranteze alınmış halini inceleyelim.
Örnek İfadeler:
a8 + a7 = a7 . (a + 1)
124 – 94 + 64 = 34 . (44 – 34 + 24)
10n+2 – 10n+1 – 10n-1 = 10n-1 . (103 – 102 – 1)
23-x + 21-x = 21-x . (23 – 1)
9n – 6n = 3n . (3n – 2n)
Dikkat ettiyseniz yukarıdaki örnek üslü ifadelerin tümünde tabandaki sayıların mutlaka ortak çarpanı var. İşte bu üslü ifadelerde toplama işlemini ortak paranteze alarak yazabildik. Yapacağınız bu minik hamle ile sorunun neredeyse %90’ını çözmüş olursunuz.
Üslü ifadelerde toplama işlemi ile ilgili güzel bir soru çözelim.
ÖRNEK 3:
( 9n + 6n ) / ( 6n + 4n ) = 8/27
denklemini sağlayan n kaçtır?
ÇÖZÜM:
Hem pay hem de payda kısmındaki üslü sayılarda toplama işlemine giren sayıları ortak paranteze alalım.
Pay kısmını 3n , payda kısmını 2n ortak parantezine alabiliriz.
3n.( 3n + 2n ) / 2n. ( 3n + 2n ) = 8/27
Pay ve paydadaki 3n + 2n ifadeleri sadeleşir.
3n / 2n = 8/27
(3/2)n = 8/27 olduğuna göre
n = -3 bulunur.
Bunu görmelisin
Tabanları farklı üslü sayılarda toplama / çıkarma nasıl yapılır?
Üslü sayılarda toplama ya da çıkarma işleminin ortak parantezle yapılabilmesi için tabanların aynı olması şart değil. Tabanları farklı olan üslü ifadelerde de toplama işlemini yapabiliriz. Yeter ki tabanların ortak böleni (çarpanı) olsun. Üstelik üssün (yani kuvvetin) aynı olmasına da gerek yok.
Hatta bazı toplama / çıkarma işlemlerinde ufak tefek bir kaç düzenleme yaparak da tabanları farklı görünen üslü isayıların aynı taban olması sağlanabilir. Aşağıdaki örneği inceleyin.
84 + 46 toplamının yarısı kaçtır?
1. yol:
Normalde tabanlar aynı olmadığı için direkt toplama yapamayız. Fakat hem 8 hem de 4 sayısının ortak böleni 4 olduğu için ortak paranteze alarak sonuca gidebiliriz.
44.(24 + 42)
44. 32 = 28 . 25 = 213
olur. Bunun yarısını alırsak sonucu
213 / 2 = 212 buluruz.
2. yol
Oysa tabanlardaki 8 ve 4 sayılarının her ikisi de 2’nin kuvveti cinsinden yazılsaydı sonuca daha kısa sürede ulaşabilirdik.
84 + 46 = (23)4 + (22)6
212 + 212 = 2. 212 olur.
Bunun da yarısını alırsak sonucu 212 buluruz.
Tabanları farklı üslü ifadelerde toplama/çıkarma işlemine örnekler
- 915 – 2710 (Burada tabanları farklı ama, her ikisi de 3’ün kuvveti şeklinde düzenlenirse tabanlar aynı olur.)
- 203 + 403 + 603 (Tabanları farklı olan bu üslü sayılarda ortak en büyük çarpan 20 olduğu için ifadeyi 203 parantezine alabiliriz.)
- (9a)4-(6a)4 = 65 (Her iki üslü ifadede tabanlar farklı olmasına rağmen ortak çarpanları 30 olduğu için (3a)4 ortak parantezine alabiliriz.)
- 15n – 10n ( Tabanları farklı üslü iki ifadede çıkarma yapmak için her ikisinde ortak çarpanın 5 olduğunu görmeniz yeterli. Burada çıkarma işleminde 5n ortak parantezine almalıyız.)
Bunu görmelisin
Tabanı ve üssü aynı olan sayılarda toplama nasıl olur?
Bu belki de en işlemi en çabuk biten üslü sayılarda toplama işlemidir. Çünkü bildiğimiz elma-armut toplaması yapmaktan farklı değil. Toplama ve çıkarmaya giren üslü sayıların tabanı ve üssü aynı ise bunları elma gibi düşünüp toplama/çıkarma işlemini çok kolay yapabilirsiniz.
Tabanı ve üssü aynı olan sayılarda toplama / çıkarma işlemine örnekler
- 38 + 38 + 38 toplamında her bir terimin tabanı ve üssü aynı. Yani 38 i elma gibi görürsek üç tane elmanın toplamı 3.(elma) olur. Yani sonuç 3.38 yani 39 olur.
- 85 + 85 + 85 + 85 toplamı 4 tane 85 in toplamında oluştuğu için sonucu 4.(85) olur. Bu işlemi biraz daha düzenlerseniz sonucun en sade biçimi 22.215 = 217 olur.
- 6.1012 + 9.1012 – 5.1012 toplamını isterseniz 1012 parantezine alarak, isterseniz 1012 yi elma gibi düşünerek çözebilirsiniz.
Üslü sayılarda çıkarma / toplama testi (9 soru)
Soru – 1

Cevap A
Soru – 2

Cevap E
Soru – 3

Cevap D
Soru – 4
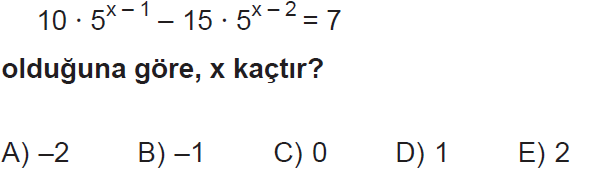
Cevap D
Soru – 5
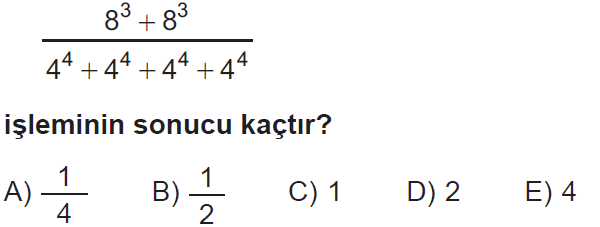
Cevap C
Soru – 6

Cevap C
Soru – 7

Cevap D
Soru – 8
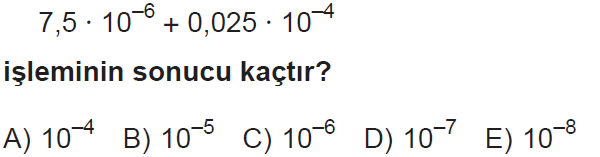
Cevap B
Soru – 9

Cevap A
Soru – 10
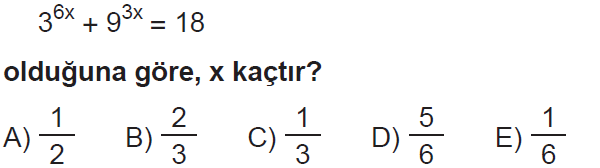
Cevap C
Dış Kaynaklar
- Üslü sayılarda toplama çıkarma (matematikkolay.net)
- Üslü sayılarda toplama işleminde tabanlar aynı ise üsler ne yapılır? (enpopulersorular.com)


 by
by 

