Üslü Sayılarda Çarpma ve Bölme

1. Üslü sayılarda çarpma / bölme yapabilmek için
2. Üslü ifadelerde çarpma ve bölmenin koşulu
3. Çarpma işleminin kuralı
4. Tabanları aynı olan üslü sayılarda çarpma
5. Tabanları farklı üsleri aynı olan üslü sayılarda çarpma
6. Tabanları ve üsleri farklı üslü sayılarda çarpma
7. Bölme işleminin kuralı
8. Tabanları aynı olan üslü sayılarda bölme
9. Tabanları farklı üsleri aynı olan üslü sayılarda bölme
10. Tabanları ve üsleri farklı üslü sayılarda bölme
11. Rasyonel üslü sayılarda çarpma / bölme nasıl yapılır?
12. Üslü sayılar bölüm testi

Bu sayfada üslü sayılarda çarpma ve bölme işlemlerini birlikte inceleyeceğiz. Zaten üslü sayılarda çarpma işlemi yapmak ile üslü sayılarda bölme yapmak birbirine o kadar benziyor ki, hem uygulaması kolay hem de akılda tutması.

Üslü sayılarda çarpma / bölme yapabilmek için

Her gördüğümüz, karşımıza çıkan her üslü sayıları ya da ifadeleri öyle kafamıza göre direk çarpamazsınız ya da bölemezsiniz. Üslü sayılarda çarpma / bölme yapabilmenin iki koşulu var. Daha doğrusu iki koşuldan her hangi birinin sağlanmış olması yeterli. Peki nedir bu koşullar?

Üslü ifadelerde çarpma ve bölmenin koşulu

Üslü ifadelerde çarpma ya da bölme yapabilmek için

• ya tabanlar aynı olmalı
• ya da üsler (kuvvet) aynı olmalı

“Hem taban hem de üsler eşit olsa olmaz mı peki?” Olur tabii ki, yeter ki biri (ya taban ya da üs) eşit olsun, fazla mal göz çıkarmaz. Diyelim ki üslü sayıların tabanın ya da üssün eşit olması sağladık. Peki nedir üslü ifadelerde çarpma ve bölmenin kuralı? Hemen anlatalım.

Çarpma işleminin kuralı

Üslü ifadelerde çarpma işlemini, tabanlardan ve üslerden hangisinin eşit olduğuna göre yaparız. Eğer hiç biri eşit değilse, birini eşit olacak şekilde düzenlememiz gerekebilir.

i) Tabanları aynı olan üslü sayılarda çarpma

Tabanları aynı olan üslü ifadelerde çarpma işlemi “taban aynı kalır üsler toplanır” kuralına göre yapılır. Yani tabanı aynı olan üslü ifadelerde, ortak taban altında üsleri toplayarak çarpma işlemi yapmalısınız.

a^x . a^y = a^x+y

Örnek çarpma işlemleri

3⁴. 3⁵. 3⁶ = 3⁴⁺⁵⁺⁶ = 3¹⁵

5⁶. 2⁵. 5⁴. 2⁷ = 5⁶⁺⁴. 2⁵⁺⁷ = 5¹⁰ . 2¹²

(2/3)². (2/3)⁴. (2/3)^-3 = (2/3)^2+4-3 = (2/3)³

ii)Tabanları farklı üsleri aynı olan üslü sayılarda çarpma

Tabanları farklı ve üsleri aynı olan üslü sayılarda “üsler aynı kalır, tabanlar çarpılır” kuralına göre çarpma işlemi yapılır. Yani kuvveti (üssü) aynı olan üslü ifadelerin, ortak üs altında tabanlarını çarpmalısınız.

a^x . b^x = (a . b)^x

Örnek işlemler:

2⁶ . 5⁶ = (2 . 5)⁶ = 10⁶

2⁵. 3⁵ . 5⁵ = (2 . 3 . 5)⁵ = 30⁵

a³. b³. c³. d³ = (a.b.c.d)³

iii)Tabanları ve üsleri farklı üslü sayılarda çarpma

Hem taban hem de üs farklı olduğunda genel olarak tabanları aynı sayının kuvveti halinde yazılıp yazılamayacağına bakarız. Tabanları aynı yaptıktan sonra üsleri toplayarak çarpma işlemini yaparız. Genellikle tabanları aynı asal sayıların kuvveti şeklinde düzenleriz.

Örneğin

• 2, 4, 8, 16, 32, 64, 128, …. sayıları 2’nin
• 3, 9, 27, 81, 243, 729, …. sayıları ise 3’ün
• 5, 25, 125, 625, …. sayıları 5’in
• 10, 100, 1000, 10000, .. sayıları 10’un

pozitif kuvveti olarak yazılabilir.

= 2⁵ .2^{15 .} 5¹⁵ = 32. (2.5)¹⁵ = 32.10¹⁰

Sayfanın sonundaki bölüm testinde bununla ilgili Soru 8 çözmeyi deneyin.

Örneğin:

8³ . 4⁵ = (2³)³ . (2²)⁵ = 2⁹ . 2¹⁰ = 2¹⁹

Eğer tabanlar aynı sayının kuvveti halinde yazılamıyorsa, o zaman mecburen üsleri aynı olacak şekilde ufak bir düzenleme yapmamız gerekebilir. Düzenlemeyi şöyle yapmalıyız.

Kuvveti küçük olana dokunmuyoruz. Kuvveti büyük olan sayıyı, kuvveti küçük olanla eşit olacak şekilde iki sayının çarpımı halinde yazmalıyız.

Örnek 1

5⁸. 2⁶ = 5². 5⁶. 2⁶ = 25.(5.2)⁶ = 25.10⁶

Örnek 2

2¹⁵. 3⁸ = 2⁷ . 2⁸. 3⁸ = 128. (2.3)⁸ = 128.6⁶

Örnek 3

32⁴. 125⁵ = (2⁵)⁴. (5³)⁵ = 2²⁰ . 5¹⁵

= 2⁵ .2^{15 .} 5¹⁵ = 32. (2.5)¹⁵ = 32.10¹⁰

Sayfanın sonundaki bölüm testinde bununla ilgili Soru 6 çözmeyi deneyin.

Bölme işleminin kuralı

Üslü sayılarda bölme işlemini, tabanlardan ve üslerden hangilerinin aynı (eşit) olduğuna göre yaparız. Eğer taban ya da üslerden hiçbiri eşit değilse, o zaman bunlardan birini birbirine eşit olacak şekilde düzenlemek gerekir.

i) Tabanları aynı olan üslü sayılarda bölme

Üslü ifadelerin tabanları eşit ise “taban aynı kalır üsler çıkarılır” kuralına göre bölme yapılır. Yani tabanları aynı olan üslü ifadelerde, aynı tabanda üsleri “üsttekinden alttakini” çıkaracak şekilde bölme işlemi yapmalısınız.

a^x : a^y = a^{x – y}

Örnek işlemler

3¹⁰ : 3⁶ = 3^10-6 = 3⁴

2⁵ : 2⁷ = 2^{5 – 7} = 2^-2

5³ : 3^-2 = 5^{3 – (-2)} = 3⁵

(1/2)⁴ : (1/2)⁹ = (1/2)^{4 – 9} = (1/2)^-5 = (2)⁵

ii) Tabanları farklı üsleri aynı olan üslü sayılarda bölme

Tabanları farklı ve üsleri aynı olan üslü ifadelerde “üsler aynı kalır, tabanlar bölünür” kuralına göre bölme yapılır. Yani aynı kuvveti (üssü) olan üslü sayıları, ortak üs altında (pay/payda)^üs şeklinde yazmalsınız.

a^x : b^x = (a : b)^x

Örnek işlemler

6⁵ : 3⁵ = (6 : 3)⁵ = 2⁵ = 32

12³ : 8³ = (12 : 8)³ = (3/2)³

10⁶ : 5⁶ = (10 : 5)⁶ = (2)⁶ = 64

iii) Tabanları ve üsleri farklı üslü sayılarda bölme

Tıpkı çarpma işleminde olduğu gibi tabanlar ve kuvvetler farklı ise genel olarak tabandaki sayıları aynı sayının kuvveti halinde yazıp yazamayacağımıza bakarız. Tabanları eşit yaptıktan sonra kuvvetleri birbirinden bölme işlemini tamamlarız

Örneğin :

27³ : 9⁴ = (3³)³ : (3²)⁴ = 3⁹ : 3⁸ = 3^9-8 = 3

Eğer tabanlar aynı sayının kuvveti halinde yazılamıyorsa, o zaman mecburen üsleri aynı olacak şekilde ufak bir düzenleme yapmamız gerekebilir. Düzenlemeyi şöyle yapmalıyız.

Kuvveti küçük olana dokunmuyoruz. Kuvveti büyük olan sayıyı, kuvveti küçük olanla eşit olacak şekilde iki sayının bölümü halinde yazabiliriz.

Örnek 1

6⁷. 3⁶ = (6. 6⁶) / 3⁶ = 6.(6 / 3)⁶ = 6.2⁶

Örnek 2

5¹⁰/ 10⁸ = (5² . 5⁸ ): 10⁸ = 25. (5/10)⁸ = 25. (1/2)⁸

Örnek 3

100⁵ / 5⁸ = (10²)⁵ / 5⁸ = 10¹⁰ . 5⁸

= (10² . 10⁸) / 5⁸ = 10² . (10/5)⁸ = 100.2⁸

Rasyonel üslü sayılarda çarpma / bölme nasıl yapılır?

Üslü ifadelerle çarpma ya da bölme işlemi yapabilmek için rasyonel sayı olmaları engel her hangi bir engel teşkil etmez. Daha önce de söylediğimiz gibi “ya tabanlar ya da üsler aynı” olursa yeterli olacaktır. O halde rasyonel üslü ifadelerin de çarpma/bölme işlemini aynı mantıkla yapacağız.

SORU:

(9/4)⁵ . (2/3)⁸ işlemini sonucu kaçtır?

[(3/2)²]⁵.(2/3)⁸ = (3/2)¹⁰.(3/2)^-8 = (3/2)² = 9/4

Dikkat ettiyseniz 9/4 ile 2/3 sayılarının ikisi de 3/2 nin tam kuvveti olarak yazılabiliyor.

SORU:

(8/125)³ . (25/4)⁵ işleminin sonucu kaçtır?

[(2/5)³]³. [(5/2)²]⁵ = (2/5)⁹.(5/2)¹⁰

= (5/2)^-9.(5/2)¹⁰ = 5/2 olur.

Üslü Sayılar Bölüm Testi

Soru-1

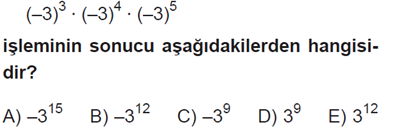
Cevap E

Soru 1’de çarpma işlemini yapmadan önce tüm işlemin işaretini belirmeniz işini kolaylaştırır. İşareti belirledikten sonra sanki, hiç birinin önünde eksi işareti yokmuş gibi çarpma işlemini yapın. Zaten sonucun kesinlikle 3¹² ya da -3¹² çıkacağı çok belli. Tüm mesele sonucun işaretini bulmakta.

Soru-2

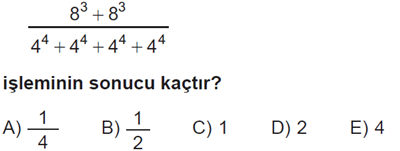
Cevap C

Soru 2’de pay ve payda kısmında üslü sayılarda toplama işlemleri göze çarpıyor. Bu toplama işlemlerini yaptıktan sonra karşınıza önce üslü sayıların çarpımı, sonraki aşamada ise bölme işlemi gelecek. Sonuçta iki tane 8³ ün toplamı ile dört tane 4⁴ ün oranını hesaplayacağız, hepsi bu.

Soru-3

Cevap B

Soru 3’te iki farklı yolda gidebilirsiniz. Birincisi, ondalık sayıları rasyonele çevirerek ilerlemek. İkincisi, 0,04’ü (0,2)² şeklinde yazıp çözmek. Birinci yol biraz daha uzundur, ama görmesi ikinci yola göre daha kolaydır. İkinci çözümü fark ederseniz soruyu çabuk çözersiniz. Fakat önce 0,04 sayısının 0,2 sayısının karesi olduğunu görmeniz gerek.

Soru-4

Cevap B

Tunç Kurt Matematik kanalından konumuzla ilgili size farklı bakış açısı katması açısından iki soru ekledik. Soruyu önce kendiniz çözmeye çalışın. Konunu kuralları belli zaten, çok zor değil. Zorlanırsanız çözümüne hemen sorudan sonraki videodan bakabilirsiniz.

Soru – 5

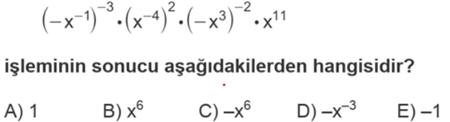
Çözüm:

Soru – 6

Çözüm:

Soru – 7

Bıyıklı Matematik kanalında Selim hocamızın anlatımıyla öğretici güzel bir üslü sayı sorusu. Aman işaretlere dikkat edelim.

Çözüm:

Soru – 8

Soruda verilen üslü ifadeleri 2’nin kuvveti şeklinde düzenlerseniz çözüme kolaylıkla ulaşırsınız. Eğer zorlanırsanız, sorunun çözümünü Selim hocanın anlatımıyla aşağıda görebilirsiniz..

Çözüm: