Üslü sayılarda sıralama nasıl yapılır? Diğer konularda yaptığımız gibi yapabilir miyiz? Cevabı kısmen evet. Çünkü üslü ifadelerde sıralama yaparken diğerleriyle aynı olmasa da benzer mantıkla ilerleriz. İşin sırrı sayı türünden çok “sıralama” kelimesinde yatıyor.
Aklınıza gelen tüm sıralama türlerini gözünüzün önüne getirin, hepsinde aynı mantık kullandığımızı fark edersiniz. Sıralamayı yapabilmek için karşılaştırdığımız sayıların bir şeyleri aynı ya da benzer olursa daha kolay sıralama yapabiliyoruz.
Üslü sayılarda sıralama nasıl yapılır?
Sıralamak istediğiniz üslü ifadeler, aşağıdaki adımlardan hangisine uyuyorsa o adımda anlatılan yolu izleyin. Bu, sizi sonuca daha çabuk götürür.
- Hesaplanması kolay olan üslü sayılarda sıralama
- Tabanları aynı olan üslü ifadelerde sıralama
- Kuvvetleri aynı olan üslü sayılarda sıralama
- Tabanları ve kuvveti farklı olan üslü sayılarda sıralama
- Tabanları ya da kuvveti harfli üslü ifadelerde sıralama
Şimdi bazılarınızın “hesap makinesi bu işi yapmaya yetiyor uğraşmaya ne gerek var” dediğini de duyar gibiyiz. Hesap makinesi kullanmak isteyenlere bir sözümüz yok elbette, dilediğinizi yapabilirsiniz. Fakat biz burada kendi imkanıyla üslü sayıları karşılaştırmak, küçükten büyüğe ya da büyükten küçüğe sıralamayı öğrenmek isteyenlere yol göstereceğiz.
Gelin hep beraber üslü sayıların sıralaması nasıl olur görelim.
1. Hesaplanması kolay olan üslü sayılarda sıralama
Adı üstünde “hesaplaması kolay” olduğu için üslü ifadelerin her birini tek tek hesaplayıp sıralayabiliriz. Örneğin 33, 25 ve 42 sayılarını sıralamak için tabanları ya da kuvvetlerini aynı yapmak gibi bir zahmete girmeseniz de olur. Çünkü bu üslü sayılar aşağıdaki gibi bir kaç basit çarpma işlemiyle kolaylıkla hesaplanabilir.
33 = 3.3.3 = 27
25 = 2.2.2.2.2 = 32
42 = 4.4 = 16
Fakat örneğin 37, 94 ve 272 gibi sayıları hesaplamak için zahmet gerekecek. Üstelik bunlar çok da büyük sayılar değiller. Bunlar gibi üslü sayılarda sıralama yapmak için aşağıdaki adımlardan hangisine uyuyorsa onu kullanmalıyız.
ÖRNEK: a = (-2)3, b = 5-1 ve c= -32 sayılarını küçükten büyüğe doğru sıralayalım.
ÇÖZÜM:
a = (-2) . (-2) . (-2) = -8
b = 5-1 = 1/5
c = – 3 . 3 = -9
O halde bu üslü sayılarda küçükten büyüğe doğru sıralama yaparsak c<a<b buluruz.
Buna bakmalısın:
2. Tabanları aynı olan üslü ifadelerde
Tabanları aynı olan üslü sayılarda kuvveti büyük olan daha büyüktür. Aman çok dikkat edin, çünkü böyle bir kesin durum yoktur. Tabanın pozitif ya da negatif olması, hatta tamsayı ya da ondalık sayı olması bile sıralamanın yönünü 180 derece çevirebilir.
Tabanlar eşit ve 1’den büyükse
Sıralanacak üslü sayıların tabanları eşit ve 1’den büyükse, kuvveti büyük olan üslü ifade daha büyük olur.
Aşağıdaki örnekleri inceleyin.
58 > 57 > 56
(6,5)10 > (6,5)9 > (6,5)8
(7/2)6 > (7/2) 5 > (7/2) 4
3-5 > 3-6 > 3-7
Tabanlar eşit ve 0 ile 1 arasında ise
an üslü ifadesinde 0<a<1 durumu varsa yani sıralanacak üslü ifadelerin tabanları eşit ve 0 ile 1 arasında basit bir kesir ise, kuvveti büyük olan üslü ifade daha küçük olur.
Aşağıdaki örnekleri inceleyin.
(0,75)4 < (0,75) 3 < (0,75) 2
(0,5)10 < (0,5)9 < (0,5)8
(2/3)6 < (2/3) 5 < (2/3) 4
(0,2)-5 < (0,2)-6 < (0,2)-7
0 ile 1 arasındaki sayıların kuvveti arttıkça sayının değeri daima küçülür.
Tabanlar eşit ve -1 ile 0 arasında ise
an üslü ifadesinde -1<a<a durumu varsa yani sıralanacak üslü ifadelerin tabanları eşit ve -1 ile 0 arasında kuvvetin tek ya da çift olmasına dikkat etmelisiniz. Kuvveti çift ise pozitif, tek ise negatif bir sayım elde edeceğiniz için çok dikkat edin.
Yani yukarıda gibi “-1 ile 0 arasındaki sayıların kuvveti arttıkça üslü sayının değeri daima küçülür” gibi kesin yargıya varmayın. Çünkü taban pozitifken durum farklıydı. Aşağıdaki örnek sıralamaları inceleyin, fikriniz olacaktır.
(-0,1)6 > ( -0,1 )4 > ( -0,1 )2
(-0,5)9 > (-0,5)7 > (-0,5)5
(-3/4)6 < (-3/4)8 < (-3/4) 10
(-2/5)3 < (-2/5)5 < (-2/5)7
(-0,4)2 > (-0,4)5 > (-0,4)3
Negatif ondalık üslü ifadeleri sıralarken, sanki pozitifmiş gibi sıralama yapın Daha sonra bulduğunuz sıralamanın yönünü çevirerek de sonuca gidebilirsiniz.
3. Kuvvetleri aynı olan üslü sayılarda
Kuvvetleri aynı olan üslü sayılarda sıralama yapmak nispeten diğerlerine göre daha kolay. Üslü ifadenin kuvvetinin pozitif ya da negatif olması önemli. Böyle bir durumda aşağıdaki gibi yapın.
Üslü sayıları sıralarken;
- Kuvveti pozitifse kuvvet (üs) yokmuş gibi sıralamanız yeterlidir. Yani ne gördüysen o.
- Kuvveti negatifse o zaman sanki kuvveti (üssü) pozitifmiş gibi sırala, sonra bulduğun sıralamanın yönünü tersine çevir.
Aşağıda verile üslü sayıların sıralamasını inceleyin.
715 > 615 > 515
(3,5)10 > (2,75)10 > (2)10
(6/5)8 > (5/4)8 > (4/3)8
6-5 > 7-5 > 8-5
Buna bakmalısın
4. Tabanları ve kuvveti farklı olan üslü sayılarda
Bu çok sık karşılaştığımız bir durum. Aslında ufak bir düzenleme yaptığınızda ilk iki maddedeki sıralama sorularına benzer. Ya taban ya da kuvvet aynı olacak şekilde üslü sayıları yeniden düzenlersek sırlama yapmak daha kolay olur.
Örneğin 46 ile 84 sayılarında hem tabanlar hem de kuvvetler farklı. Oysa bu durum bizim üslü sayılarda sıralama yapmamıza engel değil. Tek yapmanız gereken tabanı ya da kuvveti aynı olacak şekilde bu sayıları yeniden yazmak.
Tabanları aynı yaparsak;
46 = (22)6 = 212
84 = (23)4 = 212
46 ile 84 sayılarının ikisi de 212 olduğu için birbirine eşittirler.
Üsleri (kuvvet) aynı yaparsak;
46 = (43)2 = 642
84 = (82)2 = 642
Gördüğünüz gibi üsleri aynı yaptığımızda, sayılar bu şekilde de aynı çıktılar.
5. Tabanları ya da kuvveti harfli üslü ifadelerde
Tabanları ya da üsleri harfli olan üslü sayılarda sıralama işlemi tamamen taban ya da üssün ne olduğuna göre değişir. Kesin bir şey söylemek mümkün değil. Hakkında tereddüt etmeden “kesindir” diyebileceğimiz tek harfli üslü ifade şudur:
1n = 1 (Her zaman doğru)
Bir sayının sıfırıncı kuvveti yani a0 bile her zaman 1’e eşit olmayabilir. Bu yüzden harfli olan üslü ifadelerde sıralama yaparken kesinlik bildiren ifadelere çok dikkat edin.
Negatif üslü sayılarda sıralama nasıl olur?
Bir sayının üssünün yani kuvvetinin negatif olması sayısının işaretinin etkilemez, ama sayı çarpmaya göre ters döneceği için sıralamanın yönü değişir.
Normalde diyelim elimizde a3 > b3 gibi bir sıralama olsun. Üsler negatif olduğunda sıralamanın yönü tersine döner, yani
a-3 < b-3
gibi olur. Burada a ve b sayılarının sıfırdan farklı herhangi iki reel sayı olduğunu kabul ettik. Negatif üslü sayılarda sıralama yapmak pozitif üslerde sıralama yapmaktan farksızdır.
Özel Sıralama Sorusu
Soru: 320 mi 230 mu daha büyüktür?
Çözüm: 320 daha büyüktür, çünkü iki sayının kuvvetini aynı yaptığımızda
(32)10 = 910
(23)10 = 810
olur. Üsler aynı olduğu için tabanı büyük olan kazanır. Yani 32 > 23 olduğu için
320 > 230
sıralamasını elde ederiz.
Üslü Sayılarda Sıralama Testi
SORU 1:

Cevap : B
SORU 2:
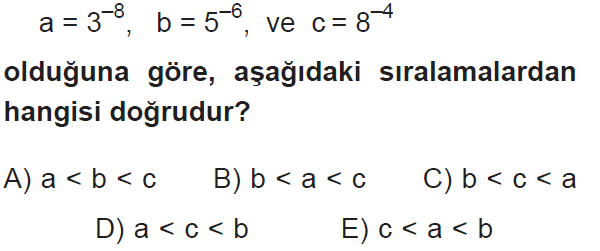
Cevap : B
SORU 3:

Cevap : A


 by
by 

